
Attribute control charts arise when items are compared with some standard and then are classified as to whether they meet the standard or not. The control chart is used to determine if the rate of nonconforming product is stable and detect when a deviation from stability has occurred. The argument can be made that a LCL should not exist, since rates of nonconforming product outside the LCL is in fact a good thing; we WANT low rates of nonconforming product. However, if we treat these LCL violations as simply another search for an assignable cause, we may learn for the drop in nonconformities rate and be able to permanently improve the process.
The c Chart measures the number of nonconformities per “unit” and is denoted by c. This “unit” is commonly referred to as an inspection unit and may be “per day” or “per square foot” of some other predetermined sensible rate.
Steps in Constructing a c Chart
- Determine cbar.
- Since the mean and variance of the underlying Poisson distribution are equal,
- Plot the centerline cbar, the LCL and UCL, and the process measurements c(i).
- Interpret the control chart.

There are k inspection units and c(i) is the number of nonconformities in the ith sample.
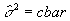
Thus,

and the UCL and LCL are:

Example:
Farnum Example: data is from Farnum (1994): Modern Statistical Quality Control and Improvement, p. 248 Non-conforming Day Errors/1000 lines 1 6 2 7 3 7 4 6 5 8 6 6 7 5 8 8 9 1 10 6 11 2 12 5 13 5 14 4 15 3 16 3 17 2 18 0 19 0 20 1 21 2 22 5 23 1 24 7 25 7 26 1 27 5 28 5 29 8 30 8 Calculations: CBAR = 4.4667 UCL = cbar + 3*sqrt(cbar) = 10.80701366 LCL = cbar - 3*sqrt(cbar) = -1.873680327 = 0 (when LCL < 0, set LCL = 0) Day CL UCL LCL NonConforming 1 4.4667 10.80701366 0 6 2 4.4667 10.80701366 0 7 3 4.4667 10.80701366 0 7 4 4.4667 10.80701366 0 6 5 4.4667 10.80701366 0 8 6 4.4667 10.80701366 0 6 7 4.4667 10.80701366 0 5 8 4.4667 10.80701366 0 8 9 4.4667 10.80701366 0 1 10 4.4667 10.80701366 0 6 11 4.4667 10.80701366 0 2 12 4.4667 10.80701366 0 5 13 4.4667 10.80701366 0 5 14 4.4667 10.80701366 0 4 15 4.4667 10.80701366 0 3 16 4.4667 10.80701366 0 3 17 4.4667 10.80701366 0 2 18 4.4667 10.80701366 0 0 19 4.4667 10.80701366 0 0 20 4.4667 10.80701366 0 1 21 4.4667 10.80701366 0 2 22 4.4667 10.80701366 0 5 23 4.4667 10.80701366 0 1 24 4.4667 10.80701366 0 7 25 4.4667 10.80701366 0 7 26 4.4667 10.80701366 0 1 27 4.4667 10.80701366 0 5 28 4.4667 10.80701366 0 5 29 4.4667 10.80701366 0 8 30 4.4667 10.80701366 0 8
c – Chart:
