
In order to prove that a process has been improved, you must measure the process capability before and after improvements are implemented. This allows you to quantify the process improvement (e.g., defect reduction or productivity increase) and translate the effects into an estimated financial result – something business leaders can understand and appreciate. If data is not readily available for the process, how many members of the population should be selected to ensure that the population is properly represented? If data has been collected, how do you determine if you have enough data?
Determining sample size is a very important issue because samples that are too large may waste time, resources and money, while samples that are too small may lead to inaccurate results. In many cases, we can easily determine the minimum sample size needed to estimate a process parameter, such as the population mean ![]() .
.
When sample data is collected and the sample mean 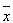 is calculated, that sample mean is typically different from the population mean
is calculated, that sample mean is typically different from the population mean 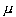 . This difference between the sample and population means can be thought of as an error. The margin of error
. This difference between the sample and population means can be thought of as an error. The margin of error 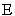 is the maximum difference between the observed sample mean
is the maximum difference between the observed sample mean 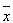 and the true value of the population mean
and the true value of the population mean 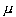 :
:
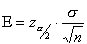
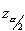 is known as the critical value, the positive
is known as the critical value, the positive 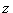 value that is at the vertical boundary for the area of
value that is at the vertical boundary for the area of 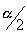 in the right tail of the standard normal distribution.
in the right tail of the standard normal distribution.
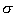 is the population standard deviation.
is the population standard deviation.
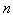 is the sample size.
is the sample size.
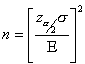
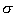 and want to determine the sample size necessary to establish, with a confidence of
and want to determine the sample size necessary to establish, with a confidence of 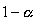 , the mean value
, the mean value 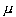 to within
to within 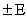 . You can still use this formula if you don’t know your population standard deviation
. You can still use this formula if you don’t know your population standard deviation 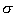 and you have a small sample size. Although it’s unlikely that you know
and you have a small sample size. Although it’s unlikely that you know 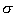 when the population mean is not known, you may be able to determine
when the population mean is not known, you may be able to determine 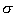 from a similar process or from a pilot test/simulation.
from a similar process or from a pilot test/simulation.
Let’s put all this statistical mumbo-jumbo to work. Take for example that we would like to start an Internet service provider (ISP) and need to estimate the average Internet usage of households in one week for our business plan and model.
Sample Size Calculation Example
Problem
We would like to start an ISP and need to estimate the average Internet usage of households in one week for our business plan and model. How many households must we randomly select to be 95 percent sure that the sample mean is within 1 minute of the population mean 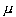 . Assume that a previous survey of household usage has shown
. Assume that a previous survey of household usage has shown 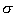 = 6.95 minutes.
= 6.95 minutes.
Solution
We are solving for the sample size 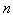 .
.
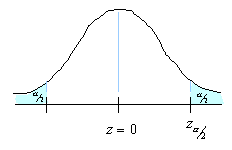
A 95% degree confidence corresponds to 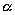 = 0.05. Each of the shaded tails in the following figure has an area of
= 0.05. Each of the shaded tails in the following figure has an area of 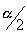 = 0.025. The region to the left of
= 0.025. The region to the left of 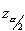 and to the right of
and to the right of 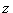 = 0 is 0.5 – 0.025, or 0.475. In the table of the standard normal (
= 0 is 0.5 – 0.025, or 0.475. In the table of the standard normal (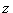 ) distribution, an area of 0.475 corresponds to a
) distribution, an area of 0.475 corresponds to a 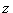 value of 1.96. The critical value is therefore
value of 1.96. The critical value is therefore 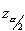 = 1.96.
= 1.96.

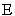 = 1 and the standard deviation
= 1 and the standard deviation 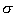 = 6.95. Using the formula for sample size, we can calculate
= 6.95. Using the formula for sample size, we can calculate 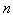 :
:
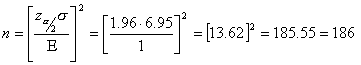
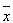 will be within 1 minute of the true population of Internet usage.
will be within 1 minute of the true population of Internet usage.
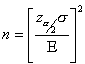
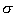 and want to determine the sample size necessary to establish, with a confidence of
and want to determine the sample size necessary to establish, with a confidence of 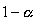 , the mean value
, the mean value 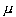 to within
to within 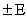 . You can still use this formula if you don’t know your population standard deviation
. You can still use this formula if you don’t know your population standard deviation 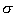 and you have a small sample size. Although it is unlikely that you know
and you have a small sample size. Although it is unlikely that you know 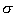 when the population mean is not known, you may be able to determine
when the population mean is not known, you may be able to determine 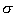 from a similar process or from a pilot test/simulation.
from a similar process or from a pilot test/simulation.