
Everyone has experienced waiting in line, whether at a fast-food restaurant, on the phone for technical help, at the doctor’s office or in the drive-through lane of a bank. Sometimes, it is a pleasant experience, but many times it can be extremely frustrating for both the customer and the store manager. Given the intensity of competition today, a customer waiting too long in line is potentially a lost customer. Understanding the nature of lines or “queues” and learning how to manage them is one of the most important areas in operations management.
Queues are basic to both external (customer-facing) and internal business processes, which include staffing, scheduling and inventory levels. For this reason, businesses often utilize queuing theory as a competitive advantage. Fortunately, Six Sigma professionals – through their knowledge of probability distributions, process mapping and basic process improvement techniques – can help organizations design and implement robust queuing models to create this competitive advantage.
The Cost of Waiting in Line
The problem in virtually every queuing situation is a trade-off decision. The manager must weigh the added cost of providing more rapid service (i.e., more checkout counters, more production staff) against the inherent cost of waiting. For example, if employees are spending their time manually entering data, a business manager or process improvement expert could compare the cost of investing in bar-code scanners against the benefits of increased productivity. Likewise, if customers are walking away disgusted because of insufficient customer support personnel, the business could compare the cost of hiring more staff to the value of increased revenues and maintaining customer loyalty.
The relationship between service capacity and queuing cost can be expressed graphically (Figure 1). Initially, the cost of waiting in line is at a maximum when the organization is at minimal service capacity. As service capacity increases, there is a reduction in the number of customers in the line and in their wait times, which decreases queuing cost. The optimal total cost is found at the intersection between the service capacity and waiting line curves.
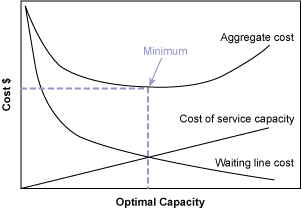
Source: Richard B. Chase and Nicholas J. Aquilano, Production and Operations Management, 1973, page 131.
Queuing Theory
Queuing theory, the mathematical study of waiting in lines, is a branch of operations research because the results often are used when making business decisions about the resources needed to provide service. At its most basic level, queuing theory involves arrivals at a facility (i.e., computer store, pharmacy, bank) and service requirements of that facility (i.e., technicians, pharmacists, tellers). The number of arrivals generally fluctuates over the course of the hours that the facility is available for business (Figure 2).
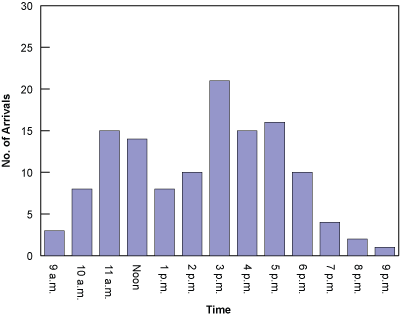
Customers demand varying degrees of service, some of which can exceed normal capacity (Figure 3). The store manager or business owner can exercise some control over arrivals. For example, the simplest arrival-control mechanism is the posting of business hours. Other common techniques include lowering prices on typically slow days to balance customer traffic throughout the week and establishing appointments with specific times for customers. The point is that queues are within the control of the system management and design.
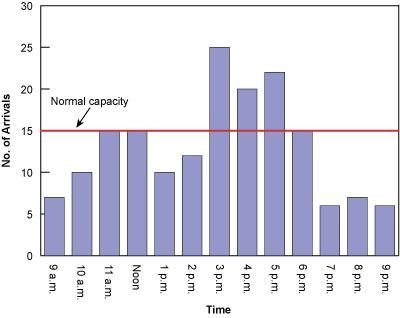
Queuing management consists of three major components:
- How customers arrive
- How customers are serviced
- The condition of the customer exiting the system
Arrivals: Arrivals are divided into two types:
- Constant – exactly the same time period between successive arrivals (i.e., machine controlled).
- Variable – random arrival distributions, which is a much more common form of arrival.
A good rule of thumb to remember the two distributions is that time between arrivals is exponentially distributed and the numbers of arrivals per unit of time is Poisson distributed.
The Servicing or Queuing System: The servicing or queuing system consists of the line(s) and the available number of servers. Factors to consider include the line length, number of lines and the queue discipline. Queue discipline is the priority rule, or rules, for determining the order of service to customers in a waiting line. One of the most common used priority rules is “first come, first served” (FCFS). Others include a reservations first, treatment via triage (i.e., emergency rooms of hospitals), highest-profit customer first, largest orders first, “best” customers first and longest wait-time first. An important feature of the waiting structure is the time the customer spends with the server once the service has started. This is referred to as the service rate: the capacity of the server in numbers of units per time period (i.e., 15 orders per hour).
Another important aspect of the servicing system is the line structure. There are four types: single-channel/single-phase; single-channel/multi-phase; multi-channel/single-phase; and multi-channel/multi-phase. The simplest type of waiting line structure is the single-channel, single-phase. Here, there is only one channel for arriving customers and one phase of the service system. An example is the drive-through window of a dry-cleaning store or bank.
Exit: There are two possible outcomes after a customer is served. The customer is either satisfied or not satisfied and requires re-service.
Waiting Line Models and Equations
Table 1 shows the four types of commonly used waiting line models, along with key properties and examples.
Table 1: Four Types of Waiting Line Models
| Model | Layout | Service Phase | Source Population | Arrival Pattern | Queue Discipline | Service Pattern | Example |
| 1 | Single channel | Single | Infinite | Poisson | FCFS | Exponential | Drive-through drycleaners |
| 2 | Single channel | Multi-phase | Infinite | Poisson | FCFS | Constant | Automatic car wash (vacuum, wetting, washing, rinsing, drying window cleaning, parking) |
| 3 | Multi-channel | Single | Infinite | Poisson | FCFS | Exponential | Teller windows in a bank; multi-lane toll road |
| 4 | Single channel | Single | Finite | Poisson | FCFS | Exponential | Machine breakdown and repair in factory |
Some of the most basic questions a Six Sigma professional will want to ask when assessing and improving a business’s waiting line model include:
- What is the utilization of the worker(s)?
- What is the average number of customers in the waiting line?
- What is the average number of customers in the system?
- What is the average wait time for customers in line?
- What is the average wait time for customers in the system (including service time)?
If a practitioner knows the arrival rate (λ) and the service rate (µ) of their customers, they can easily calculate the answers to these questions using the formulas in Table 2.
Table 2: Equations for Line Calculations
| Key Questions | Equation |
| What is the utilization of the worker(s)? | Ï = λ / µ |
| What is the average number of customers in the line? | nt = λ2 / µ (µ – λ) |
| What is the average number of customers in the system (time spent in line and service time)? | ns = λ / µ – λ |
| What is the average wait time for custsomers in line? | tt = λ / µ (µ – λ) |
| What is the average wait time for customers in the system (time spent in line and service time)? | ts = 1 / µ – λ |
Rite Aid Case Study
In March 2010, Rite Aid Pharmacy introduced a bold new marketing promotion strategy: Rite Aid will fill your prescriptions in 15 minutes, guaranteed (customers are given a $5 Rite Aid Gift Card for prescriptions not filled within 15 minutes). To understand how Rite Aid could make such a guarantee, I visited a few stores in the Atlanta metro area, where I live. As a good Six Sigma practitioner, I carefully watched the process of how prescriptions were filled, talked with the employees and took notes. Rite Aid uses a single-channel/multi-phase queuing model with one technician and one pharmacist. Prescription filling is not a serial process. While the technician is handling customers (drop off and pick up), the pharmacist fills prescriptions. Table 3 reflects the high-level, three-step process and key activities.
Table 3: Prescription Filling Process
| Drop-off (Technition) | Fill Prescription (Pharmacist) | Pick-up (Technition) |
| • Verify prescription (patient full name, DOB, medication name and dosage, and physician’s signature)
• Check insurance coverage • Check available inventory |
• Enter prescription information into PC
• Checks medication against patient profile and prescription • Generates prescription label • Retrieves ulk medicine bottle from shelf • Counts appropriate amount of medicine • Pours into a bottle • Affix label to bottle |
• Instructions for taking medicine, explain side effects
• Customer signature • Technician collects payment |
To get a comprehensive understanding of the process, I visited the stores at various times throughout the week and weekend and observed the customer arrival rates and pharmacy service rates. At peak times, I observed upward of 20 customers per hour arriving (λ) at the pharmacy. Not all, however, would qualify for Rite Aid’s prescription guarantee. (The guarantee applies to orders of three prescriptions or fewer and prescriptions that do not require prior authorization.) Occasionally, the medication was not in inventory. Other times, prescriptions required prior-authorization by the insurance company. Sometimes, customers simply asked the technician for general store information. On one occasion, I observed a customer applying for more than three prescriptions. These conditions combined to bring the number of qualified customers down to 16. Technicians were able to service a customer in about three minutes (including drop off and pick up) or a service rate (µ) of 20. The ratio of refills to new prescriptions averaged 70:30. Clearly, new prescriptions took a little longer than the refills.
Assuming Poisson arrivals and exponential service for this case, my first question was to understand the utilization rate (Ï) of the customer-facing technician. Using the formula, Ï = λ / µ, I calculated 80 percent [16 ÷ 20]. This seemed about right considering that the technician must also answer the phone and handle miscellaneous questions regarding insurance and other products. Utilization rates of 100 percent or more should serve as red flags to Six Sigma professionals to re-assess the process and staffing levels.
The average number of customers in the queue was slightly more than three [162 ÷ 20 (20-16)], while the average number of customers waiting in the system was four [16 ÷ 20 – 16]. Based on my observations, these figures made sense considering peak times.
The next set of questions relate to waiting time. The average waiting time for a customer in line was 12 minutes [16 ÷ 20 (20 – 16) x 60 minutes]. However, this metric did not explain the whole story. I needed to determine the average wait time for customers in the system (time spent waiting in line, plus service time). Using the formula, ts = 1 ÷ µ – λ, I arrived at 15 minutes [1 ÷ 20 – 16) x 60 minutes]. I could have also arrived at this answer by summing up 12 minutes plus 3 minutes (service rate).
From my cursory analysis using queuing model equations, I was able to see how Rite Aid could make such a bold guarantee. If Rite Aid wanted to reduce the waiting time to, say, 10 minutes, they could either reduce the arrival rate (i.e., get customers “out-of-line” by encouraging prescriptions through telephone or email; embrace the use of automatic prescription routing from the doctor via e-commerce applications) or improve the service rate through technology (i.e., robotic pharmacy dispensing systems).
Putting Theory to Use
Queuing theory is not just some esoteric branch of operations research used by mathematicians. It is a practical operations management technique that is commonly used to determine staffing, scheduling and inventory levels, and to improve customer satisfaction. By understanding queues and learning how to manage them through simple models and equations, Six Sigma practitioners can help improve customer-facing and internal processes to give organizations a competitive advantage.