Part 1 in this series on software defect metrics discussed Goals 1 and 2, which focused on identifying and removing defects in the development process as close to the point of occurrence as possible (Table 1). This installment looks at predicting defect insertion and removal dynamics early in a project and measuring predicted versus actual defect find rates during each development stage. The next and final installment in the series provides a foundation for understanding the most elusive metrics, defect density measures such as defects per million opportunities (DPMO).

Goal 3: Predict Defect Find and Fix Rates During Development and After Release

Classifying and counting defects helps focus problem solving and root cause analysis efforts, however can quantify defect history in a somewhat static way. Historical defect data can assist organizations early in the project planning process to predict defect insertion and find defect counts for each development stage or iteration step. Beyond predictive tallies, it is also important to recognize the rate at which defects accumulate. Predicting both dynamics can add sensitivity to the defect diagnosis on a new project, and support project staffing plans.

Defect insertion and removal dynamics over the course of a development project are summarized in Figure 1. The left curve illustrates that defect insertion (in the form of ambiguities, misunderstandings, omissions, etc.) begins when the project effort begins, during the earliest stages of the fuzzy front end. Defects are often tied to the intensity of the effort (e.g., number of people involved, lines of communication, decisions being made, etc.) and the insertion rate usually tracks with that contour.

The second curve illustrates that finding and fixing defects most often occurs substantially after the work-product effort. For an organization depending on the final test process to find most defects, this lag can have a negative impact. Activities like peer reviews and inspections find defects closer to their insertion point, shifting the find curve to the left, where the fix times and costs are lower.

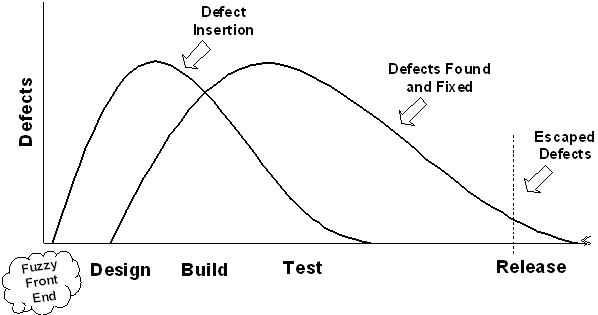
The asymmetry in the curves suggests that it takes more time to get done than it did to get engaged. The Rayleigh Model¹ is a proven method to predict and track this time-dynamic. Here its use is extended to predict defect find and fix rates.

Starting Simple – Using Project History

Collecting data on the effort, duration, work-product size, and defect counts for a number of projects provides an opportunity to analyze trends, ultimately resulting in more accurate predictions for new projects. Project teams lacking trend data can still get started by using industry benchmarks as a guide. Generally speaking, if a team does not know “where they are” they probably are not doing any better than representative industry averages. Applying those averages as deemed appropriate can provide a reasonable place to begin the estimating process. As each project progresses, a continual review of predicted versus actual defect counts will allow the team to refine the estimates and improve the model for the next project.

Figure 2 illustrates a case where the project team estimated the size of the new project at about 1,250 Function Points.² Two additional inputs are included, one that assess the organization’s Productivity Index³ and one that anticipates schedule compression. These inputs will drive project deadlines. The model computes estimates of duration, effort, and defects as total, pre-release and released figures.

Applying the most likely scenario, the second line in the figure with a total defect estimate of 946, to a scorecard facilitates the next level of detailed predictions (Figure 3), Goals 1 and 2 provided the ability to understand and quantify phase containment effectiveness (PCE), defect containment effectiveness (DCE) and insertion rates. Those numbers take on a predictive value in the scorecard, where they are used to distribute the total defect count across development or iteration steps.

Building on the measurements enabled through Goals 1 and 2, project teams can use their growing database of phase containment data to estimate the number of defects expected in each phase of a new project.

The circle in Figure 3 highlights the number of defects expected during the requirements stage. As development progresses the predicted versus actual defect tallies are compared. Cases where the actual is significantly higher than predicted may provide early warning of a problem. Actual tallies that are much less than predicted should prompt an investigation to ensure that leaks in the defect detection methods are not present before determining that the insertion rate was lowered.

Defect Time Contouring With the Rayleigh Model

The Rayleigh distribution offers a useful fit to real-world experience and data. The model requires two inputs, the overall total quantity contoured over time (K) and the time period necessary to estimate the quantity. The quantities most often modeled for software projects are effort and defects. The total (K) for each of these is easily estimated early in the project and the Rayleigh Model can readily provide a view of their distribution over time.

Numbers for total effort and total defects are derived from the estimating model (Figure 2). These totals, together with an anticipated time to reach peak estimate are the only quantities needed to compute the Rayleigh curve (Figure 4). For the defect plot, an additional value associated with the estimated lag behind the start of the project effort is needed to account for defect find and fix work.

The pair of curves in Figure 5 illustrates the time-dynamic connection between project effort and defects. The Model provides support for fact-based discussions about the impact of changes such as accelerating the project delivery date. For a project under pressure to deliver within 9 months, the Model will clearly display that many defects will still remain. The Model facilitates analysis of the cost of delivering those defects versus the advantages of early delivery.

The Model’s cumulative distribution function (CDF) supports a more refined discussion of the impact associated with a change in delivery date. This figure describes the total-to-date effort expended or defects found at each interval. Figures 6, 7, and 8 show the Rayleigh CDF formula, chart and values table respectively.

Figures 7 and 8 provide quantitative, fact-based data to support a discussion on the delivery date. At 12 months the Rayleigh Model indicates the expectation that 96.9 percent of the defects are found. Moving delivery to 9 months could reduce the total containment effectiveness (TCE) to around 81.6 percent. An organization about to make that decision is well advised to weigh the benefits of early delivery against the costs associated with released defect repair and possibly, customer loyalty that are involved in that tradeoff.

Looking Ahead to Part 3

Defect counts and classifications by phase or activity, and over time provide a basic analysis platform that supports a number of Six Sigma goals as applied to software. These basic measures fail to account for differences in the size or complexity of the work products. The last two goals in our metrics maturity table call for the comparison of implementations within the company and across companies. In each case, defect density normalization is needed.

Goal 4: Compare Implementations Within the Company

Defects per unit size as defined within the company can support fair comparisons between projects and groups.

Goal 5: Benchmark Implementations Across Companies

Making comparisons across companies calls for a more universal approach to defect density normalization. This is the reason that defects per million opportunities (DPMO) was developed for Six Sigma manufacturing environments. While the approach is not simple science, it is applicable to explore the fundamentals of the DPMO concept within the software development environment.

Read Six Sigma Software Metrics, Part 3 »

Footnotes and References
1 The Rayleigh model is special case of the Weibull distributions. A good treatment of the general topic, with software application examples, can be found in Kan, Stephen, Metrics and Models in Software Quality Engineering. Addison-Wesley, 2003.
2 See www.ifpug.com, www.spr.com, and/or the work of Capers Jones for more information on Function Point sizing.
3 See Six Sigma Meets Project Management