
Because of corporate collapses such as Enron and WorldCom, large financial institutions during the last decade have had to absorb enormous losses. In the wake of these fiscal disasters, financial organizations needed to develop risk-rating scorecards to help them become much more quantitative in how they evaluate and assign risks. Six Sigma can provide a path to better risk-rating scorecards.
Some risk-rating scorecards use actuarial models to predict the likelihood that a given business will default based on different types of financial risk – economic (inflation, market, interest rate, credit, liquidity, etc.), political, compliance, security and regulatory.
Historically, risk ratings were developed from a probability curve that risk analysts would generate based on data from a large universe or population of a particular type of business. They would assign a number to a business based on several criteria to generate a total risk score, and compare that score with the default probability (Figure 1). They would then manually adjust the three “pivot points” on the model (top, mid and bottom) to better match the characteristics of the actual companies being evaluated. The adjustment was based primarily on experience, or what can be translated as “gut feeling.”

The sideway bell curves in Figure 1 indicate that the pivot points could vary as much as plus or minus 10 percent. That means the gut-feeling method obviously was not working well.
Addressing the Calibration Challenge
One large national bank employs a commercial risk-rating scorecard which, as the name implies, is used when making loans to commercial entities (as opposed to individuals). When the bank found it was losing millions of dollars each year, it realized that its risk scorecard was inaccurate and imprecise – leading to incorrect estimation of risk ratings, increased volatility of credit losses and inaccurate pricing of commercial loans. The bank wanted to come up with a quantitative method for adjusting the curve so that it could refine the general population model to better match the risk characteristics of the specific companies it was evaluating.
To calibrate its estimates of commercial credit losses, the bank decided to apply basic Six Sigma DMAIC (Define, Measure, Analyze, Improve, Contro) framework. Six Sigma is great at reducing variation – improving both accuracy and precision, which are key attributes of a measurement process. The goal of the Six Sigma project was to create a more accurate and precise scorecard, which would enable the bank to make more accurate loan pricing estimates, in turn reducing losses for bad credit. The project team applied some advanced statistical techniques, the details of which are beyond the scope of this article. But the key points can be reviewed.
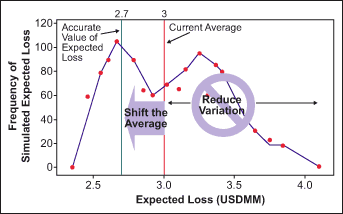
How Far Off Is the Current Risk Rating?
The team’s first step was to try to quantify just how far off the current risk-rating method was. To do this, it simulated the process of assigning risks and making commercial loans to a set of known businesses. The team then compared the “expected losses” from these companies against an industry standard metric for those same companies. The results are shown in Figure 2. As can be seen, there was a lot of variability in the expected loss (the blue line with red dots) – from about $2 million to more than $4 million. Also, the current average loss was nearly $300,000 greater than what the industry standard said should be expected (compare the red line to the green line).
The green line represents the benchmark risk, what is known as the KMV Implied Risk Rating. KMV is a private firm based in San Francisco that provides forecasts of estimated default probabilities using a market-based approach to credit risk. Recovery rates and correlations across default also are factored into the model, thus making it a relatively robust estimate of the current state of a firm. (Though the KMV value was used as a benchmark, the bank did not want to use it in risk calculations because it reflects the characteristics of an entire population of businesses, not the specific businesses the bank wants to evaluate.)
This simulation verified that the bank’s current method was both inaccurate (giving higher expected losses than it should) and imprecise (had a lot of variability). The bank’s goals were to reduce variation (see less spread in the estimates) and shift the average, as reflected in the figure.
The Approach: Constrained Optimization
A person buying a car usually looks for the best choice based on the various factors they need to balance, which statisticians call constraints. The factors might include how much money the person has to spend, gas mileage, type of car, resale value, power, passenger capacity and so on. Some factors are more important than others, so they are given more weight – for example, price might outweigh mileage. This approach of balancing weighted factors to find an optimal choice is called “constrained optimization.”
The same concept applies when developing a risk-rating scorecard. The bank needed a method of evaluating risk that would give it better control over the risk probability curve shown in Figure 1 – in other words, a method that would let the bank adjust the pivot points, which in turn determine how it assigned risk and what it charged for commercial loans. Project team members came up with five constraints they would use to quantify how optimal the new risk assignment method was:
- Directional shift: This is an estimate of the amount that a credit rating moves under the new model compared to the original calibration method. It includes the direction of the movement. For instance, if the original method assigned a rating of 6 to a particular company and the new method assigns a risk of 4, the directional shift is -2.
- Distance: The distance is the absolute value of the shift in ratings between the two methods. Using the example above, the distance of the particular company would be 2.
- Number of outliers: If a credit risk improves by more than one whole risk rating, it is an upgrade outlier. If it goes down by more than one risk rating, it is a downgrade outlier. The total number of outliers is the sum of upgrade and downgrade outliers.
- Shifting in 8s and 9s: Under the bank’s scoring system, companies in Categories 8 and 9 represent the highest credit risk. Watching for shifts in these categories is a measure of important outliers. Understanding any changes in this area of the scorecard is paramount to accurately assessing risk.
- Granularity: Under the original model, commercial applicants were assigned a risk rating of 1 to 9. The bank felt it would benefit if it could get more granularity, that is, have more divisions in the rating.

Testing the New Risk-Rating Method
The team created weights for the above factors using an analytical hierarchy process, a tool commonly used in Design for Lean Six Sigma. This blended function was then used to create the “best” top, middle and bottom anchors in calibrating the curve shown in Figure 1.
To test this new method for improvement, the team first compared the variation in the pivot points to the original variation. The result is shown in Figure 3.
As shown in the figure, the variation became plus or minus 2 percent versus the original plus or minus 10 percent. But what impact does this 8-percent reduction in variation have on the risk-rating scorecard? The team tested the new method by calculating new ratings for 61 companies that had already been assigned a risk rating under the old method.
The comparison between the old and new ratings is shown in Table 1. The table compares risk ratings for 61 companies under the old system (rows) and the new system (columns). As can be seen, the new system has 18 categories versus only nine in the original system. This is the increased granularity the bank was looking for. Numbers in the darker blue bands indicate companies that essentially got the same rating though they may have shifted slightly due to the increased number of rating categories (for example, four of the original 5s became 5+). Numbers in the lighter blue bands or outside the blue areas represent more substantial shifts in ratings.
| Table 1: Comparison of Ratings Using Old and New Systems | ||||||||||||||||||||
|
Risk Rating Generated by Proposed Scorecard |
||||||||||||||||||||
| Existing Risk Rating |
1 |
2 |
3 |
4+ |
4 |
4- |
5+ |
5 |
5- |
6+ |
6 |
6- |
7+ |
7 |
7- |
8 |
9+ |
9 |
Percentage |
Totals |
|
1 |
0% |
0 |
||||||||||||||||||
|
2 |
1 |
2% |
1 |
|||||||||||||||||
|
3 |
1 |
1 |
1 |
1 |
7% |
4 |
||||||||||||||
|
4 |
1 |
1 |
1 |
1 |
7% |
4 |
||||||||||||||
|
5 |
2 |
2 |
4 |
3 |
1 |
1 |
1 |
2 |
26% |
16 |
||||||||||
|
6 |
1 |
2 |
1 |
2 |
2 |
2 |
1 |
4 |
1 |
1 |
1 |
30% |
18 |
|||||||
|
7 |
1 |
5 |
2 |
1 |
15% |
9 |
||||||||||||||
|
8 |
4 |
8% |
5 |
|||||||||||||||||
|
9 |
1 |
2 |
1 |
7% |
4 |
|||||||||||||||
| Percentage |
0% |
0% |
3% |
0% |
7% |
5% |
10% |
3% |
8% |
5% |
7% |
3% |
3% |
11% |
13% |
16% |
5% |
0% |
100% |
61 |
| Totals |
0 |
0 |
2 |
0 |
4 |
3 |
6 |
2 |
5 |
3 |
4 |
2 |
2 |
7 |
8 |
10 |
3 |
0 |
61 |
|

Using the same simulation technique for the baseline in the Measure phase, the team performed a few more simulations from various industries. Figure 4 illustrates the improvements using the blended optimization calibration. Again, the green line represents the benchmark credit loss from KMV. The new method’s average (middle blue line) is quite close to the benchmark. That means the team has improved the accuracy of the model.
There also is a substantial reduction in variation, as shown by the location of the 10th and 90th percentile bands, which translates into improved precision. Some 80 percent of the new risk evaluations will fall between those two bands. Compare that spread to the width of the original estimates in Figure 2.
The Results: Applying to Other Portfolios
Once the team tested this new method, a user guide and training program was created to ensure that all risk analysts had this new tool and were comfortable with the new method of calibrating risk scorecards. To help gain acceptance, the team noted the risk improvements for three specific companies in the energy portfolio. Below are the results:
| Table 2: Risk Improvements for Three Companies | |||||
Company |
Old Method |
New Method |
Benchmark KMV |
Old Method |
New Method |
|
DYN |
5 |
6.67 |
7.33 |
-2.33 |
-0.66 |
| ENR |
4 |
7 |
8.67 |
-4.67 |
-1.67 |
| HAL |
3 |
6.67 |
6.67 |
-3.67 |
0 |
The total underestimation of risk for the original method was 10.67 risk-rating points compared to a total underestimation of only 2.33 risk-rating points using the new method. That means the new method allows the bank to generate much better estimates of risk, and therefore make better decisions in giving credit to commercial firms. The bank is happy with this quantitative approach to evaluate its credit risk-rating process and has expanded its usage to other portfolios and applications.