Key Points
- Goodman-Kruskal Gamme is a calculation used for ordered or discrete data.
- It is used to determine whether pairs of calculations match given the p-value calculated.
- Once you have the Gamma, the closer to 1 it is, the more likely the pair is related.
The Gamma coefficient tells you how closely two pairs of ordinal data points match or are correlated. The estimator of Gamma uses the number of concordant and discordant pairs of X and Y observations. Tied pairs are ignored.
Overview: What is Goodman-Kruskal Gamma?
The Gamma statistic was first proposed in a series of papers from 1954 to 1972 by Leo Goodman and William Kruskal. Gamma can be calculated for continuous ordinal (ordered) data such as height, time, or age. It can also be used for discrete data like good, better, and best.
The calculation of Gamma is based on two quantities:
- Nc, the number of pairs where the ranked values are the same for both variables. This is called the concordant pairs.
- Nd, the number of pairs where the ranked values are in reverse order for both variables. This is called the discordant pairs.
- Ties, where the values of paired data are equal, are ignored.
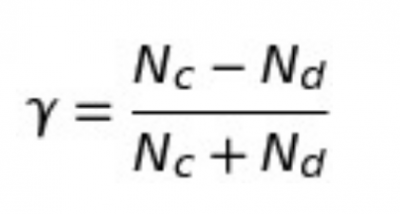
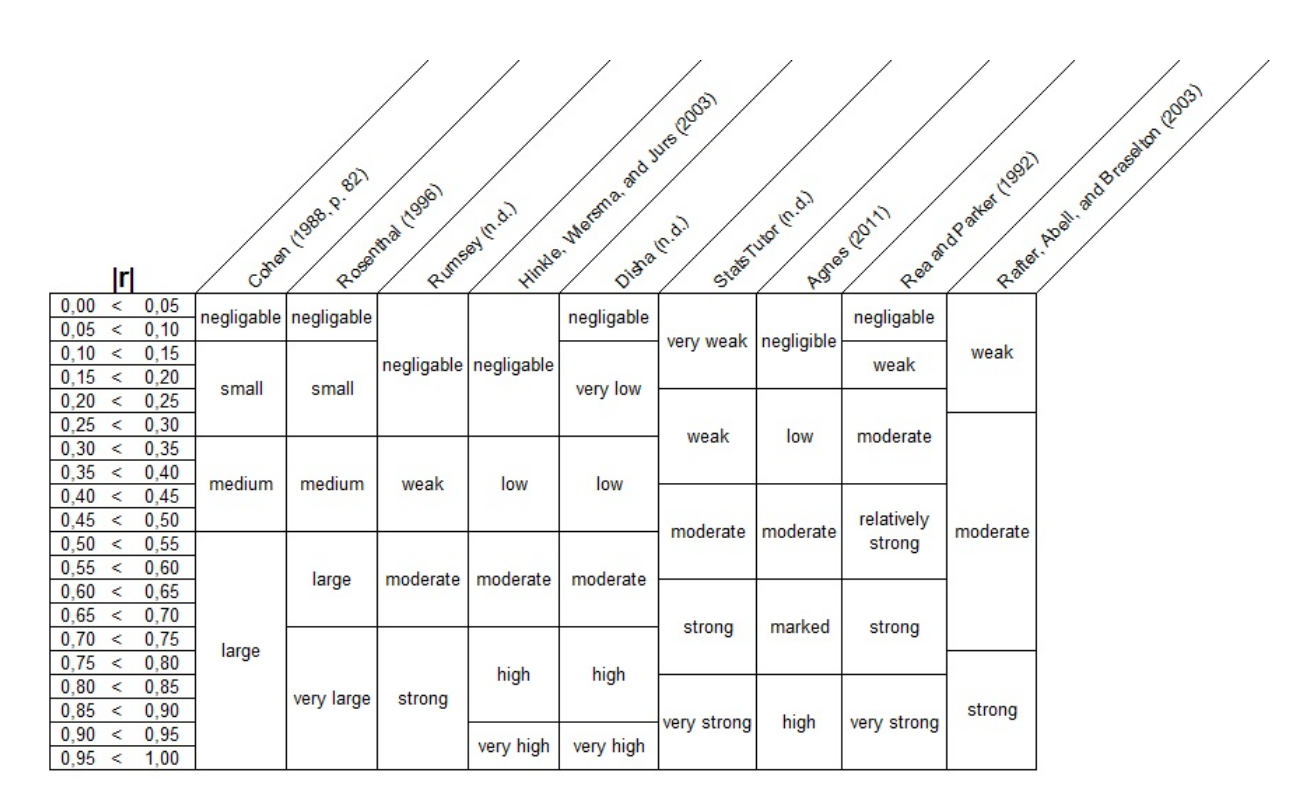
The closer you get to 1 (+1 or -1), the stronger the association or correlation. You can determine the statistical significance by calculating a p-value or using a rule of thumb. Gamma can be interpreted as the proportion of ranked concordant pairs. For example, if Gamma = +1, you can interpret that to mean every pair in your ranked data agrees and is a match. Here is a table of common rules of thumb by various authors:
Playing the Match Game
So, why does Gamma matter in the context of any sort of analysis? Having the means to directly compare based on qualitative or quantitative data takes a fair bit of the leg work out of many things. However, where Gamma shows its usefulness comes about in the form of comparing disparate data sources as shown in the industry example below.
An Industry Example of Goodman-Kruskal Gamma
HR was analyzing operator data on hours spent studying for a job-related test versus how well they did. They hypothesized that more studying should lead to better test results. A simple 2×2 contingency table was set as below:
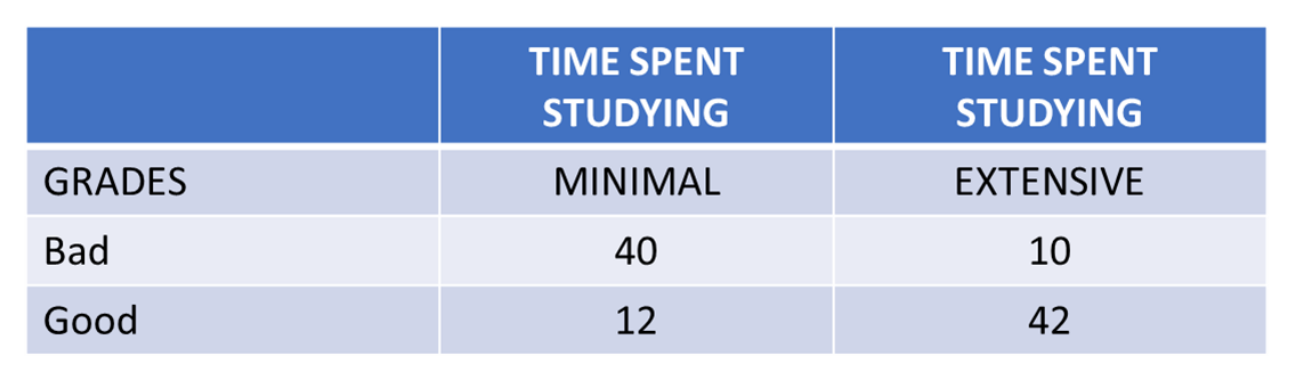
The cells for MINIMAL time/Bad scores and EXTENSIVE time/ Good scores support their hypothesis that studying and test results have an association and are concordant. The other two cells are the reverse of what would be expected.
Gamma was calculated as follows:
- Start with the concordant pairs. Nc = 40 * 42 = 1680,
- Now calculate for the discordant pairs. Nd = 10 * 12 = 120.
- The gamma statistic is:
(Nc – Nd) / (Nc + Nd) = (1680 – 120) / (1680 + 120), or 0.867.
Since the Gamma value is relatively high compared to +1, the HR manager can comfortably conclude that studying helps with test scores.
Other Useful Tools and Concepts
Hungry for more? Understanding the random variation found within any process can be instrumental in determining the overall efficiency and effectiveness of your current workflow. Randomness is going to show regardless of careful planning, but learning how to harness it can lead to better overall efficiency.
Further, you might need to brush up on Little’s Law. This is a wonderful metric for seeing how long your production is going to take to send deliverables out to your customer. To learn how to calculate it, I heavily recommend our article on the subject.