Key Points

• Control limits allow you to see extreme variations throughout your analysis.
• There are two separate control limits, with an upper and lower respectively.
• Being able to readily see where your data rests compared to the average is useful in any stage of your data analysis.

Control limits, how do they work? Is it a probability limit? Is it an economic limit? Read on to find out! 

Overview: What Are Control Limits?

A control chart consists of several parts. It has two limits. The bottom dashed line is called the lower control limit (LCL), and the top dashed line is the upper control limit (UCL). Further, the solid middle line is the average of the statistic being plotted.

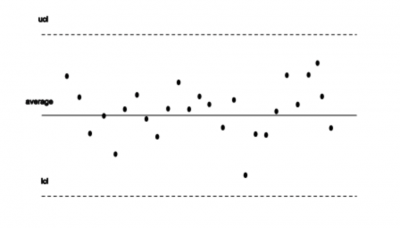
The limits are calculated from the data that is plotted on the control chart. They are placed +/-3 sigma away from the average line.

Control limits are used to mark the point beyond which a sample value is considered a special cause of variation. They are also used to define the upper and lower limits of the common cause variation.  

Benefits of Control Limits

Control limits are based on the process data itself. However, control limits do three things.

Provide You a Guide to What Is Happening in Your Process

These are not a requirement, like specification limits. Subsequently, because these measurements are based on the process measure, they give you a realistic guideline as to what to expect from the process.

Take Into Account Both the Within and Between Sample Variation

Take, for example, a control chart for the average and range. A sample consists of five-part lengths. Both the range (highest-lowest of the part lengths) and the average length of the five parts are part of the control limit formula. The range represents within and the average between the sample variation.  

Establish the Predictable Limits of Variation for the Process Measure

It provides a frame for the common cause variation when the process is stable.

Why Are Control Limits Important to Understand? 

Control limits have been around for a long time. Walter Shewhart, a physicist at Bell Laboratories, first wrote about control limits in 1924. He developed control charts to help improve the quality of telephone equipment. 

Dr. Shewhart spent years of research conducting many, many experiments to simulate various production outputs. 

Based on the results of these experiments, and Tchebycheff’s theorem, Dr. Shewhart decided to place control limits at +/- 3 sigma of an average (such as an average or range) to minimize the economic loss from two kinds of mistakes. 

(Technical Note: Tchebycheff’s theorem provides statistical support for the +/- 3 sigma limits. It states that 89% of any distribution (regardless of shape, center, and spread) will fall within +/- 3 sigma.)

• Mistake 1: Calling variation a special cause of variation when it’s a common cause of variation. This results in wasted time and effort, chasing non-existent special causes, and/or making changes that don’t help and might hurt in unexpected ways.
• Mistake 2: Calling variation a common cause when it’s a special cause variation. This results in lost opportunities. A special and fleeting source of variation in the process exists and will not be found.  

Consider Dr. Shewhart’s dilemma!

If the limits were very wide, for example, +/- 8 sigma from the average, we would never make mistake 1.  

If they were very narrow, let’s say, +/- 0.1 sigma from the average, we would never make mistake 2. 

The 3 Sigma Limits balance the probability of making both these mistakes. As such, these are the reasons Shewhart used 3-Sigma Limits. 

An Industry Example of Control Limits

In this example, a manager is using a control chart to measure the average time to answer a customer question on a helpline.

The manager collected about 20 samples of call times (three calls an hour). He uses a computer program (such as Excel) to plot the samples against the historic upper and lower control limits.

The control chart shows several call time averages to be outside the lower control limit. What can be said about the call time measure?

1. The points outside the control limit indicate special causes where the calls are shorter than would be expected. This is a positive type of special cause because the manager would like the calls to be shorter, if possible.
2. The manager should look at the process and try to understand what the source of the shorter calls might be.
3. If the source of the shorter call is found, the manager should take action so that the reason for shorter than expected calls can be integrated into the process.

The manager investigated the calls outside of the lower limit. Afterward, he found out they all had been taken by the first shift of workers. The first shift workers were found to have recently taken the new call center training.  

All shift workers were given the new training, and subsequent call time averages started to trend downward, showing that the improved training worked. 

Why It Matters

Data points only mean so much when it comes time to do some hard analysis. As such, establishing limits beyond the average allows you to readily see the extreme outliers in a given data set. While we touched on this in the industry example, this is handy for any process or production workflow. It enables you to readily hone in to see potential problem areas and implement changes as needed.

Best Practices When Thinking About Control Limits 

Recall that control limits are not probability limits — they are placed at +/- 3 sigma because that’s where they work best. These limits are one key to process improvement actions.  

Use the Standard Control Limit Formula and the Control Chart Table to Calculate the Control Limits

The control limit formula will vary depending on the statistic (average, range, proportion, count) being plotted. Ensure you are using the right formula! 

Use the Control Limits to Assess if There Is a Special Cause

If a plotted point goes beyond the upper or lower control limit, it can be considered a special cause. This means the manager/worker should act to find the source of the special cause or respond to the control plan direction for a special cause.

Use the Control Limits to Evaluate the Predicted Spread of Common Cause Variation

When the process is stable, the process measure can be expected to vary randomly between the upper and lower control limits. 

Other Useful Concepts

So, now that you’re up to speed on control limits, it’s time for some other essential reading. Why not take a moment and glance over our guide on Gage R&R to understand how to make the most of your data during the analysis stage?

Further, you might want to read up on how normality applies to data analysis. Our handy guide is a brisk read and should get your bearings on the concept in no time at all.

Final Thoughts on Control Limits

Control limits are one part of a control chart that allows you to identify common and special cause variations. If you understand how they were designed to work, then you have the key to effective process improvement.