
An organization is always successful in its journey towards business excellence if it has specific goals for each of its critical processes. Various quality management programs adopted and implemented by such an organization can streamline the activities towards the ultimate goal of business excellence. When the quality improvement program is Six Sigma, the goal for the organization is obvious – to reach a sigma level of six, or the well-known objective of 3.4 defects per million opportunities (DPMO). An organization operating at that level is described by Six Sigma proponents as being world class.
Many organizations may call themselves Six Sigma organizations as they start to implement various improvement tools of a typical Six Sigma program. But they really are not Six Sigma organizations in the sense of being world class (Table 1) until they are operating at, or at least closing in on, the goal of 3.4 DPMO. The reality is an organization can have difficulty telling exactly where it stands overall in terms of sigma level. That is because some of its critical processes are more important to its operations than others. And the sigma levels of all processes at any one time are unlikely to be the same.
| Table 1: Classification of an Organization Using Sigma Level | ||
|
Sigma |
|
Category |
|
6 |
3.4 |
World class |
|
5 4 3 |
230 6,200 67,000 |
Industry average |
|
2 1 |
310,000 700,000 |
Noncompetitive |
An approach is available to obtain the overall sigma level of an organization based on weighting each of the critical processes. Thus if a unit produced by a higher-weighted critical process is found defective, then obviously such a defective unit costs more for the operation than a defect from a lower-weighted process. This method develops a link between each critical process and the DPMO and determines an overall weight-based sigma level.
Several possible cases are explored by assigning arbitrary values to weighted processes and sigma levels to illustrate how the overall sigma level of an organization can be obtained.
Weight-based Sigma Level
In many survey-related studies on performance of organizations with regard to customer satisfaction, an organization is said to have achieved or exceeded the level of customer satisfaction, if its average score is greater than or equal to 5 when the survey is conducted using a Likert scale of 1 to 10 (1 being not satisfied and 10 being extremely satisfied). The very purpose of the quality function deployment (QFD) tool is to prioritize various processes based on the importance ratings obtained as a result of customer satisfaction and/or customer requirement surveys.
For the Malcolm Baldrige National Quality Award criteria, weights are given to each of the critical success factors (dimensions) depending on their importance. For example, according to the award’s 2004 criteria, the factors “strategic planning,” “customer and market focus,” “human resource focus” and “process management” are each given the weight of 85 points (8.5 percent), the factor “measurement, analysis and knowledge management” is allotted a weight of 90 points (9 percent), the factor “leadership” has a weight of 120 points (12 percent) and the factor “business results” is given the maximum of 450 points (45 percent). Hence, the attempt to adopt this aspect in categorizing all the critical processes of an organization by giving specific weights to them in a clear way so as to obtain an overall weight-based sigma level of the organization at a given point of time.
Let us consider xi (i = 1, 2, … , n) are the n critical processes identified by the organization of interest. At a point of time, let k1, k2, …, kn are the sigma levels of the processes x1, x2, … , xn respectively. Extensive study on the importance of these processes may reveal specific weights for the critical processes. Let w1, w2, …, wn be the weights assigned to the respective processes such that:
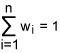
This implies that the process xi assumes a weight wi to each unit produced, either defective or non-defective. Now the overall sigma level of an organization with regard to all n critical processes is obtained by using the information from Table 2.
| Table 2: Weighted Defects Per Million Opportunities | ||||
|
Critical |
Weight |
Sigma |
DPMO |
Weighted-DPMO |
|
x1 |
w1 |
k1 |
p1 |
(w1) × p1 |
|
x2 |
w2 |
k2 |
p2 |
(w2) × p2 |
|
. |
. |
. |
. |
. |
|
xn |
wn |
kn |
pn |
(wn) × pn |
The total weighted-DPMO from all the processes put together is obtained as:
![]()
The overall sigma level is now obtained for this combined DPMO either from the available tables or using the NORMSINV function available in Microsoft Excel. This sigma level is compared with Table 1 to determine the category in which the organization falls.
For a typical organization, a critical process may be higher-valued or equally-valued or lower-valued relative to other critical processes. This aspect may be easily visualized from the Baldrige criteria in which the dimensions are weighed differently or from QFD application in which relative ratings are used to prioritize the processes or process parameters for improvement. Hence, in a given set of critical processes that are used to determine the organization’s overall sigma level, all critical processes may be in the equally-valued category or few may be in the higher-valued category and hence the remaining are in the lower-valued category. Let us assume, without loss of generality that in case of equally-valued n processes the weights are equal (1/n) and hence a weight 1/n is assigned to each unit produced by any of these n processes. Obviously, when the weights are equal, we get only the average of the DPMO values as the total weighted-DPMO. However, the overall sigma level that we get ultimately is not the average of the corresponding sigma levels (refer to Tables 4, 5 and 6). When few processes (say, m < n) are higher-valued, then the weight assumed for each of the m such higher-valued processes is apparently more than that of the individual lower-valued processes. Under these circumstances the combinations shown in Table 3 may be expected.
| Table 3: Process Types, Weights and Possible Sigma Levels | |||
|
Process Type |
Weight |
Sigma Level |
|
|
Equally-Valued |
1/n |
Higher Sigma Level |
Lower Sigma Level |
|
Higher-Valued |
wi > wj * |
Higher Sigma Level |
Lower Sigma Level |
|
Lower-Valued |
wj < wi * |
Higher Sigma Level |
Lower Sigma Level |
* wi is the weight of the i-th higher-valued process out of m such processes and wj is the weight of the j-th lower-valued process out of n – m such processes.
Numerical Study
In this study we are assuming that there are five critical processes (A, B, C, D and E) identified by an organization that alone are contributing to the maximum in its journey towards Six Sigma quality and hence are having an ultimate goal of achieving business excellence. Various arbitrary weights and sigma levels are chosen in different combinations to the critical processes in order to illustrate how an overall weight-based sigma level can be calculated for the organization. Though any combination is possible, only the following six cases are considered in this numerical study (Tables 4-9):
Case I: All processes are equally-valued and resulted in higher sigma levels.
In this case, all the five processes are treated as equally important and hence each process is assumed a weight 1/5. We have considered higher (above 5) sigma levels for all the five processes. The overall sigma level is calculated using the data provided in Table 4.
| Table 4: Equally-valued Processes (Higher Sigma Levels) | ||||
|
|
|
Sigma |
DPMO |
Weighted-DPMO |
|
A |
1/5 (20%) |
6 |
3.4 |
0.68 |
|
B |
1/5 (20%) |
6 |
3.4 |
0.68 |
|
C |
1/5 (20%) |
6 |
3.4 |
0.68 |
|
D |
1/5 (20%) |
5.5 |
31.69 |
6.338 |
|
E |
1/5 (20%) |
5.25 |
88.44 |
17.688 |
From Table 4, we get total weighted-DPMO equal to:
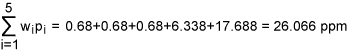
Let q = 26.066/1000000 = 0.000026066. Then the sigma quality level, k =1.5 + NORMSINV (1 – 0.000026066) = 1.5 + 4.046 = 5.546. Note that since equal weights are assigned, 26.066 ppm is nothing but the average of the respective DPMO values but 5.546 is not an average of the respective sigma levels. We conclude that the organization has achieved an overall sigma level of 5.546 and this falls in to the category of world class. On the other hand if we simply add the DPMO values the total becomes 130.33 ppm whose sigma quality level k = 1.5 + NORMSINV (1 – 0.00013033) = 1.5 + 3.652 = 5.152 which seems not reasonable.
Case II: All processes are equally-valued and resulted in lower sigma levels.
In Case II, all the five processes are treated as equally important and hence each process is assumed a weight 1/5. However, we have considered lower (between 3 and 5) sigma levels for all the five processes. The overall sigma level is calculated using the data provided in Table 5.
| Table 5: Equally-valued Processes (Lower Sigma Levels) | ||||
|
|
|
Sigma |
DPMO |
Weighted-DPMO |
|
A |
1/5 (20%) |
5 |
232.67 |
46.534 |
|
B |
1/5 (20%) |
4 |
6,209.70 |
1,241.940 |
|
C |
1/5 (20%) |
3 |
66,810.63 |
13,362.126 |
|
D |
1/5 (20%) |
3.5 |
22,750.35 |
4,550.070 |
|
E |
1/5 (20%) |
4.5 |
1,349.97 |
269.994 |
From Table 5, we get total weighted-DPMO equal to:
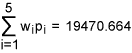
Let q = 19470.664/1000000 = 0.019470664. Then the sigma quality level, k =1.5 + NORMSINV (1 – 0.019470664) = 1.5 + 2.065 = 3.565. Hence, we conclude that the organization has achieved an overall sigma level of 3.565 and this falls in to the category of industry average.
Case III: All processes are equally-valued and two resulted in higher sigma levels and three resulted in lower sigma levels.
In case III, all the five processes are treated as equally important and hence each process is assumed a weight 1/5. We have considered two processes with higher sigma levels and the remaining three with lower sigma levels. The overall sigma level is calculated using the data provided in Table 6.
| Table 6: Equally-valued Processes (Two Higher Sigma and Three Lower Sigma Levels) | ||||
|
|
|
Sigma |
DPMO |
Weighted-DPMO |
|
A |
1/5 (20%) |
6 |
3.4 |
0.68 |
|
B |
1/5 (20%) |
6 |
3.4 |
0.68 |
|
C |
1/5 (20%) |
3 |
66,810.63 |
13,362.126 |
|
D |
1/5 (20%) |
3.5 |
22,750.35 |
4,550.070 |
|
E |
1/5 (20%) |
4.5 |
1,349.97 |
269.994 |
From Table 6, we get total weighted-DPMO equal to:
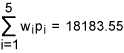
Let q = 18183.55/1000000 = 0.01818355. Then the sigma quality level, k =1.5 + NORMSINV (1 – 0.01818355) = 1.5 + 2.093 = 3.593. Hence, we conclude that the organization has achieved an overall sigma level of 3.593 and this falls in to the category of industry average. Note that in this case the organization is not coming under the category of world-class though it has achieved six-sigma level in two of the five critical processes.
Case IV: Two processes are higher-valued and three processes are lower-valued and all resulted in higher sigma levels.
In this case, two processes are treated as higher-valued with a weight of 0.30 each and the remaining three as lower-valued with weights 0.10 and 0.15. We have considered higher sigma levels for all the five processes. The overall sigma level is calculated using the data provided in Table 7.
| Table 7: Two Higher-Valued and Three Lower-Valued Processes (Higher Sigma Levels) | ||||
|
|
|
Sigma |
DPMO |
Weighted-DPMO |
|
A |
0.30 (30%) |
6 |
3.4 |
1.02 |
|
B |
0.15 (15%) |
6 |
3.4 |
0.51 |
|
C |
0.10 (10%) |
6 |
3.4 |
0.34 |
|
D |
0.15 (15%) |
5.5 |
31.69 |
4.7535 |
|
E |
0.30 (30%) |
5.25 |
88.44 |
26.532 |
From Table 7, we get total weighted-DPMO equal to:
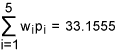
Let q = 33.1555/1000000 = 0.0000331555. Then the sigma quality level, k =1.5 + NORMSINV (1 – 0.0000331555) = 1.5 + 3.989 = 5.489. Hence, we conclude that the organization has achieved an overall sigma level of 5.489 and this falls in to the category of world class.
Case V: Two processes are higher-valued and three processes are lower-valued and all resulted in lower sigma levels.
In case V, two processes are treated as higher-valued with a weight of 0.30 each and the remaining three as lower-valued with weights 0.10 and 0.15. We have considered lower sigma levels for all five processes. The overall sigma level is calculated using the data provided in Table 8.
| Table 8: Two Higher-valued and Two Lower-valued Processes (Lower Sigma Levels) | ||||
|
|
|
Sigma |
DPMO |
Weighted-DPMO |
|
A |
0.30 (30%) |
5 |
232.67 |
69.801 |
|
B |
0.15 (15%) |
4 |
6,209.70 |
931.455 |
|
C |
0.10 (10%) |
4 |
66,810.63 |
6,681.063 |
|
D |
0.15 (15%) |
3.5 |
22,750.35 |
3,412.5525 |
|
E |
0.30 (30%) |
4.5 |
1,349.97 |
404.991 |
From Table 8, we get total weighted-DPMO equal to:
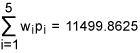
Let q = 11499.8625/1000000 = 0.0114998625. Then the sigma quality level, k =1.5 +NORMSINV (1 – 0.0114998625) = 1.5 + 2.273 = 3.773. Hence, we conclude that the organization has achieved an overall sigma level of 3.773 and this falls in to the category of industry average.
Case VI: Two processes are higher-valued and three processes are lower-valued and two resulted in higher sigma levels and three resulted in lower sigma levels.
In case VI, two processes are treated as higher-valued with a weight of 0.30 each and the remaining three as lower-valued with weights 0.10 and 0.15. We have considered two processes with higher sigma levels and the remaining three with lower sigma levels. The overall sigma level is calculated using the data provided in Table 9.
| Table 9: Two Higher-valued and Two Lower-valued Processes (Two Higher Sigma and Three Lower Sigma Levels) | ||||
|
|
|
Sigma |
DPMO |
Weighted-DPMO |
|
A |
0.30 (30%) |
6 |
3.4 |
1.02 |
|
B |
0.15 (15%) |
6 |
3.4 |
0.51 |
|
C |
0.10 (10%) |
6 |
66,810.63 |
6,681.063 |
|
D |
0.15 (15%) |
3.5 |
22,750.35 |
3,412.5525 |
|
E |
0.30 (30%) |
4.5 |
1,349.97 |
404.991 |
From Table 9, we get total weighted-DPMO equal to:
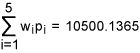
Let q = 10500.1365/1000000 = 0.0105001365. Then the sigma quality level, k =1.5 +NORMSINV (1 – 0.0105001365) = 1.5 + 2.308 = 3.808. Hence, we conclude that the organization has achieved an overall sigma level of 3.808 and this falls in to the category of industry average. Note that in this case the organization is not coming under the category of world class though it has achieved six-sigma level in two of the five critical processes.
Summary and Conclusions
When it implements a quality improvement program, an organization would like to monitor its progress at every given point of time. And, the organization notes the milestones it crosses on its journey toward business excellence. When it is a Six Sigma quality program, the milestones are the sigma levels that the organization achieves by its implementation. Obviously the organization aims for the Six Sigma goal of 3.4 DPMO. Such an organization is often referred to as a Six Sigma organization. Since, an organization can identify many critical processes that contribute to the Six Sigma status, the sigma levels of each of these processes contribute to the overall sigma level. However, each critical process may be at different levels of importance to the organization. The approach outlined here incorporates assigning weights to the critical processes and the corresponding DPMO values and hence it is effective in obtaining an accurate overall sigma level of an organization.