
For a tool that has such broad applicability, the analytical hierarchy process (AHP) is not as widely known as might be expected. AHP makes assessments, prioritization and selection among options more readily measurable. Thus it is a natural Six Sigma ally and a part of the toolkit for a growing number of practitioners. AHP, which grows out of work that was done in the field of operations research by mathematician Thomas Saaty, has evolved into a rich set of methods with assessment and prioritization at their core.
The Challenge of Prioritization
When asked to rank or rate a list of things according to some criterion, such as preference, value, risk or cost, one might be able to rank their order and even to assign some numbers to their relative positions on the list. However, two problems arise in that simple scenario:
First, whatever measurement scale is chosen is just ordinal at best. A rating of 10 does not mean the preference, risk or whatever for an item is twice that of an item rated 5. (One might be tempted to treat the numbers as a ratio scale, but there is no basis for it.)
Second, when there are more than a few items on the assessment list, it gets hard to keep all the prioritization considerations in one’s mind at the same time – making it hard to think about and to complete the task.
The AHP Answer
AHP takes that simple-enough looking prioritization problem and makes it simpler and more meaningfully measurable. First, it reduces the list into pairwise comparisons and asks for a ratio assessment of each pair. Using a simple case to illustrate, to assess preference for three features, A, B and C, AHP would set up the three pairwise comparisons (AB, AC and BC).
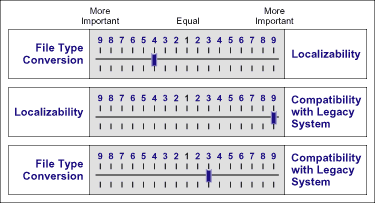
Making a relative assessment of the members of each pair is something most people find easy to do. Figure 1 traces the preference assessments for three simple requirements – File Type Conversion, Localizability and Compatibility with Legacy System.
Evaluation (Figure 1) shows File Type Conversion is somewhat more important than Localizability, 4.0 transferred to the table below. Compatibility is much more important than Localizability, 9.0 transferred to table. Compatibility is just a little more important than File Type Conversion, 3.0 transferred to table. AHP captures each assessment, and then computes the ratio-scaled priorities and an “inconsistency ratio” of 0.01, as noted in Table 1.
| Table 1: Assessments Gathered in the AHP Matrix | |||
|
File Type Conversion |
Localizability |
Compatibility with Legacy System |
|
| File Type Conversion |
4.0 |
3.0 |
|
| Localizability |
9.0 |
||
| Compatibility with Legacy System | |||
|
Inconsistency Ratio 0.01 |
|||
Assessing Inconsistency
An interesting side effect of asking a person to make a series of pairwise ratio-based comparisons is the way that they “forget” prior assessments as they go. If their understanding of the system is coherent, the whole set of pairwise comparisons should stack up in a self-consistent way. In a preference assessment, if a person places A much greater than B, then A slightly greater than C and then B slightly greater than C, they have created a set of circumstances that do not make sense as a whole. They have revealed inconsistency in their thinking on the matter. (See Figure 2.) That could show that a respondent was not paying attention or that they do not understand the dynamics of the assessment well enough to see things clearly.
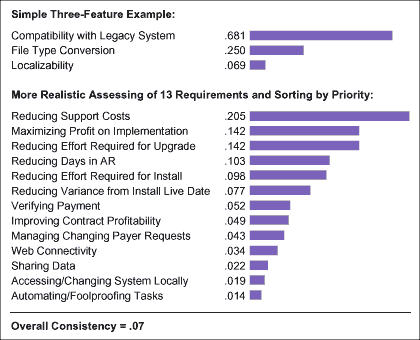
Inconsistency ratios (which involves some matrix math) of greater than about 0.1 are generally viewed as worthy of concern. Ratios smaller than 0.1 reflect a pretty coherent set of assessments. As a companion to AHP preference rankings, the inconsistency ratio provides useful guidance about how to interpret information coming back from an individual or a group.
AHP for Groups
AHP can be especially useful with groups. Each member’s assessments can, of course, be evaluated for priorities and inconsistency, and then the group rollup (and group segments) can be synthesized and viewed the same way (note the second bar graph in Figure 2). This can be a powerful way to build consensus, as each constituent can see where they stand and compare it to the group as a whole. If the group has a high inconsistency ratio (more than 0.1, or so) segmenting might reveal where the differences in agreement are and why. That, too, can help lead to better understanding and consensus.