Key Points

• Homogeneity of variance is the assumption that your data sets are equal in variance.
• It allows for the validation of conclusions for the many tests used in statistical analysis.
• It also allows you to understand Type 1 and Type 2 errors as they occur.

When doing statistical hypothesis testing, it is often assumed that the variances of your sample data groups are essentially equal. Even if you are testing for differences in means, the need to have equal variances will still be an assumption you will need to meet.

Overview: What Is Homogeneity of Variance?

Starting with the premise that you have independent and random groups of continuous data, you may use that data to answer several different statistical questions. If you have two groups of data, you might seek to determine whether the means or variances of those groups are the same or not.

In this situation, you will want to use a 2-sample t-test. While there is an assumption of normality for the two groups, the t-test can be done with an assumption of equal variance or unequal variance (Welch’s t-test).

If you have more than two groups of data and wish to determine whether the means are equal, you will use ANOVA. This test has an assumption of normality for the different groups but also an assumption of homogeneity of variance or, in other words, equal variances.

Putting It Together

While there is no normality assumption or homogeneity of variance assumption for your data groups in linear regression, they both are assumed concerning the analysis of residuals. Here, the residuals should be normally distributed and the variance constant across your range of residual values.

Fortunately, the t-test and ANOVA use the t and F statistics respectively, which are generally robust to violations of the assumption as long as group sizes are equal.  If your group sizes are vastly unequal and the homogeneity of variance is violated, then the F statistic and test will be biased.  When this occurs, the significance level will be under/overestimated, which can cause the null hypothesis to be falsely rejected and you incur a Type 1 error or you lose power in your test and have a Type 2 error and fail to reject the Ho when you should have.

Levene’s test is a common test used to determine if your sample groups have equal variances. Bartlett’s test is also used frequently to test for homogeneity of variance. The Levene test is more robust than Barlett for nonnormality. Therefore, if you have evidence that your sample data comes from an approximately normal distribution, then Bartlett is a more powerful test.

3 Benefits of Homogeneity of Variance

Your hypothesis tests and regression analyses are enhanced by meeting the assumption of homogeneity of variance.

1. Validate the Conclusions of Various Statistical Tests

The conclusions of your t-tests, ANOVA, and regression analysis will be valid if you meet the test assumptions including homogeneity of variance.

2. Avoids Problems with Type 1 Errors

By not meeting the assumption of homogeneity of variance, you may increase the probability of over or underestimating the significance and power of your test which may result in making a Type 1 or 2 error.

3. Somewhat Robust to Violation

Your assumption of homogeneity of variance may be robust to violation if your sample sizes are large enough and not too dissimilar in size.

Why It Matters

You don’t go into statistical analysis without some means of validating your outputs. That’s where homogeneity shines, at least for a few given statistical tests. It equips you with the means and ability to see where things truly lie when accounting for variances in your samples.

Why Is Homogeneity Important to Understand?

Ignoring or not properly testing for homogeneity of variance may lead to erroneous conclusions about your data.

Pooled Estimate of Variance

Some of the calculations in your hypothesis testing and regression use a pooled variance or standard deviation which assumes you’re pooling variances of approximately equal size.

Assures Distribution of Your Groups Is Essentially Equal

An equal variance will help assure you that the distributions of your samples and populations are essentially equal.

Provides Insight Into Possible Type 1 or 2 Errors

If you fail the test for equal variance, you will have some insight into whether you should be concerned about making a Type 1 or 2 error.

An Industry Example

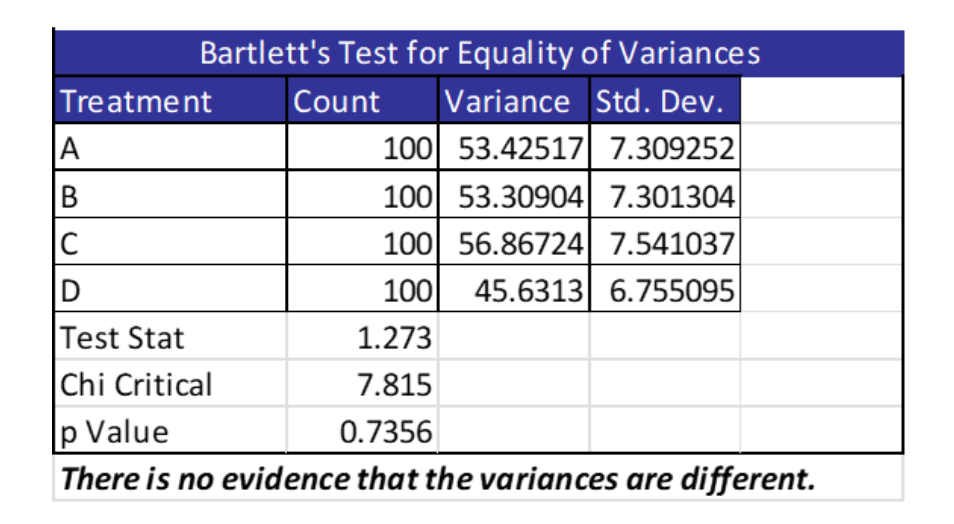
The HR Manager was reviewing turnover statistics and wanted to know if there was any statistical difference in turnover across the company’s four sites. She was advised to use ANOVA to determine if the average turnover is different. She decided to first test the assumption of homogeneity of variance. Below are the results from the statistical software she used.

Because the p-value is greater than their selected alpha risk of .05, the manager concluded the four variances are statistically equal.

3 Best Practices When Thinking About Homogeneity of Variance

Here are a few tips to help you understand how to handle homogeneity of variance.

1. Test for Homogeneity of Variance Before Testing Your Means

Often, it is best to test for all assumptions before going ahead and doing your desired statistical test. The common ones are testing the assumption of normality and homogeneity of variance.

2. Try to Obtain Group Samples of Approximately the Same Size

Varying sample sizes may impact your variance and thus the homogeneity of those group variances.

3. Consider Using Welch’s Test or a Nonparametric Test

If you fail your initial assumptions of equal variance, you can use Welch’s test where appropriate or a nonparametric test or as a last resort, transform your data.

Other Useful Tools and Concepts

Looking for other ways to bolster your business? You might want to learn about the differences between discrete and continuous data. These two very different data types are a cornerstone of statistical analysis.

Further, you might want to take a closer look at project ROI. Knowing where to invest resources, funds, and time can be daunting. However, process ROI gives some guidance on which projects are worth investing in.

Wrapping Up Homogeneity of Variance

Several statistical tools have an underlying assumption of equal variance or homogeneity of variance. If the assumption is violated, your results may not be valid. There are a variety of options and alternatives that you can use to get the answers you want despite not being compliant with the assumption of equal variance.