
One difficulty that arises when Six Sigma is applied directly to the product development process is performing meaningful experimentation on the “process” of developing a product. Often the development cycle is long and many significant project changes occur generation to generation. This makes it hard to attribute process improvements to a specific process change. One way of overcoming this difficulty is to include the wealth of information gained from a bug tracking system in the DMAIC roadmap.
Many development teams use bug, or issue, tracking systems to record all the problems with projects. These databases allow a team to log details on unsolved problems with a design, and to archive the details and status of problems already solved. These systems can be used for software, firmware or hardware, and track issues arising in any phase of development, including verification, lab testing and system testing. At the end of a project, the bug tracking system serves as a repository of all the issues encountered and descriptions of solutions for the issues. The more detailed the information the better.
Using the historical data detailed in the bug tracking system, practitioners can perform simulated experimentation – instead of the typical direct experimentation done during DMAIC – to assess the effectiveness of proposed process improvements. Simulated experimentation may provide a quicker and more efficient method than what can be achieved through direct experimentation on the product development cycle.
Save Time with Bug Tracking System
The technique described here uses simulated experimentation to replace direct experimentation typically done during DMAIC on the process under study. The critical factors and the effectiveness of proposed process improvements are assessed using the historical data detailed in the bug tracking system. This technique of using a simulated experiment may provide a quicker and more efficient method of experimentation than what can be achieved through direct experimentation on the product development cycle.
How to Get Started
The specific steps of the simulated experiment using bug tracking system information to model process improvement effectiveness are:
- Identify the set of bugs to be used as the model input.
- Detail the proposed process changes.
- For each proposed process improvement, estimate its effectiveness to catch or avoid each bug.
- Sort the matrix and review for consistency.
- Calculate the average effectiveness for each proposed process change.
- Determine the cumulative improvement.
In general, a Six Sigma project team will use its knowledge and the details from the bug tracking system to assess the effectiveness of each proposed process change against a set of past bugs. The technique then combines the individual assessments to create a prioritized ranking of the proposed process changes. The resulting prioritized ranking of the proposed process changes can be used to assess which are the most effective, or critical, and should be implemented and addressed in the Control phase.
Identify Bugs for Model Input
The first step is to determine the set of bugs that will be used for the model input. Several factors can play into this decision. The more recent the bug data used for the model input, the better. With bug records from the recent past, there is a much better chance that people who worked are the project are still with the organization and can remember the situation to provide the effectiveness estimates.
Another factor that needs to be taken into account is how well the bug data represents the current state of the process. If the process has changed significantly since the bug data used for the model input was collected, the modeling effectiveness will be limited.
The final factor to consider is whether the model inputs represent the spectrum of possible bugs. Particular types of problems may not have occurred within the bug data used for the model input. In these cases proposed process improvements that would have been effective against the missing types of problems will not be assessed adequately.
Detail Proposed Process Changes
Practitioners should spend time generating detailed descriptions of the proposed process changes. This will help the team come to a common understanding of what the proposed process changes are, and what impacts they may actually have. These details are even more valuable when others are brought in who have worked on the bugs but have not been part of the Six Sigma project team. Because these new people lack the history of how these proposed process improvements were derived, they need more details in order to provide better estimates.
Estimate the Effectiveness of Each Improvement
Now it is important to generate the actual effectiveness estimates for each combination of each bug and each proposed process change. This is the majority of the work and should be done with as much of the team as possible to maximize the experience being factored in.
To prepare for the initial meeting, the leading practitioner should put together a blank input matrix. In this example, the project has seven proposed process changes, labeled “A” through “H,” and 20 bugs, “Bug 1” through “Bug 20.” By assessing the effectiveness of each proposed process change and bug combination, the team can estimate the overall effectiveness of the seven proposed process changes.
The process for filling in the matrix is straightforward, but completing the matrix may actually take several meetings. To be as efficient as possible, all the details for the bugs should be available to the entire team while the bugs are under discussion. If others need to be pulled in who have more experience with the particular bug under discussion, those meetings should be planned and scheduled to make efficient use of everyone’s time. Anything that can be done to get participants to review bug detail prior to the meeting will speed things along.
Once the matrix is completed, it is possible to see how viable each proposed change may be (Table 1). For example, Change A has a 50 percent probability of catching Bug 1, and a 70 percent probability of catching Bug 4, and so on.
| Table 1: Completed Input Matrix | |||||||
| Proposed Process Changes | |||||||
| Bugs | A | B | C | D | E | F | G |
| Bug 1 | 50 percent | 0 percent | 0 percent | 50 percent | 0 percent | 0 percent | 0 percent |
| Bug 2 | 0 percent | 70 percent | 0 percent | 70 percent | 0 percent | 0 percent | 0 percent |
| Bug 3 | 0 percent | 0 percent | 70 percent | 60 percent | 0 percent | 0 percent | 0 percent |
| Bug 4 | 70 percent | 0 percent | 0 percent | 20 percent | 0 percent | 0 percent | 0 percent |
| Bug 5 | 0 percent | 0 percent | 60 percent | 10 percent | 0 percent | 0 percent | 90 percent |
| Bug 6 | 0 percent | 0 percent | 0 percent | 30 percent | 0 percent | 0 percent | 0 percent |
| Bug 7 | 40 percent | 0 percent | 0 percent | 40 percent | 100 percent | 0 percent | 0 percent |
| Bug 8 | 0 percent | 0 percent | 0 percent | 50 percent | 0 percent | 0 percent | 90 percent |
| Bug 9 | 0 percent | 5 percent | 0 percent | 60 percent | 0 percent | 0 percent | 90 percent |
| Bug 10 | 10 percent | 0 percent | 0 percent | 100 percent | 0 percent | 0 percent | 0 percent |
| Bug 11 | 20 percent | 0 percent | 0 percent | 100 percent | 0 percent | 40 percent | 0 percent |
| Bug 12 | 0 percent | 0 percent | 70 percent | 0 percent | 0 percent | 0 percent | 30 percent |
| Bug 13 | 40 percent | 5 percent | 0 percent | 10 percent | 0 percent | 0 percent | 100 percent |
| Bug 14 | 0 percent | 0 percent | 0 percent | 0 percent | 50 percent | 50 percent | 0 percent |
| Bug 15 | 50 percent | 0 percent | 0 percent | 0 percent | 0 percent | 50 percent | 0 percent |
| Bug 16 | 0 percent | 0 percent | 60 percent | 40 percent | 0 percent | 0 percent | 0 percent |
| Bug 17 | 90 percent | 0 percent | 0 percent | 0 percent | 70 percent | 0 percent | 0 percent |
| Bug 18 | 0 percent | 0 percent | 80 percent | 70 percent | 0 percent | 0 percent | 0 percent |
| Bug 19 | 70 percent | 0 percent | 0 percent | 0 percent | 0 percent | 0 percent | 0 percent |
| Bug 20 | 0 percent | 0 percent | 20 percent | 0 percent | 80 percent | 0 percent | 0 percent |
| Average | 22 percent | 4 percent | 18 percent | 36 percent | 15 percent | 7 percent | 20 percent |
Sort Matrix and Review for Consistency
Once the matrix has been completed, the project team can review it. As a sanity check, the table can be sorted by each individual row and column and reviewed for consistency, and necessary adjustments can be made. For example, in Table 2 the matrix has been sorted by the column for Change D. The team should review the bugs listed in the sorted column, and ensure that the bugs at the top of the list are the most likely to be caught by the proposed process change and that those at the bottom of the list are the least likely to be caught by the change.
| Table 2: Input Matrix Sorted By Proposed Process Change D | |||||||
| Proposed Process Changes | |||||||
| Bugs | A | B | C | D | E | F | G |
| Bug 10 | 10 percent | 0 percent | 0 percent | 100 percent | 0 percent | 0 percent | 0 percent |
| Bug 11 | 20 percent | 0 percent | 0 percent | 100 percent | 0 percent | 40 percent | 0 percent |
| Bug 2 | 0 percent | 70 percent | 0 percent | 70 percent | 0 percent | 0 percent | 0 percent |
| Bug 18 | 0 percent | 0 percent | 80 percent | 70 percent | 0 percent | 0 percent | 0 percent |
| Bug 3 | 0 percent | 0 percent | 70 percent | 60 percent | 0 percent | 0 percent | 0 percent |
| Bug 9 | 0 percent | 5 percent | 0 percent | 60 percent | 0 percent | 0 percent | 90 percent |
| Bug 1 | 50 percent | 0 percent | 0 percent | 50 percent | 0 percent | 0 percent | 0 percent |
| Bug 8 | 0 percent | 0 percent | 0 percent | 50 percent | 0 percent | 0 percent | 90 percent |
| Bug 7 | 40 percent | 0 percent | 0 percent | 40 percent | 100 percent | 0 percent | 0 percent |
| Bug 16 | 0 percent | 0 percent | 60 percent | 40 percent | 0 percent | 0 percent | 0 percent |
| Bug 6 | 0 percent | 0 percent | 0 percent | 30 percent | 0 percent | 0 percent | 0 percent |
| Bug 4 | 70 percent | 0 percent | 0 percent | 20 percent | 0 percent | 0 percent | 0 percent |
| Bug 5 | 0 percent | 0 percent | 60 percent | 10 percent | 0 percent | 0 percent | 90 percent |
| Bug 13 | 40 percent | 5 percent | 0 percent | 10 percent | 0 percent | 0 percent | 100 percent |
| Bug 12 | 0 percent | 0 percent | 70 percent | 0 percent | 0 percent | 0 percent | 30 percent |
| Bug 14 | 0 percent | 0 percent | 0 percent | 0 percent | 50 percent | 50 percent | 0 percent |
| Bug 15 | 50 percent | 0 percent | 0 percent | 0 percent | 0 percent | 50 percent | 0 percent |
| Bug 17 | 90 percent | 0 percent | 0 percent | 0 percent | 70 percent | 0 percent | 0 percent |
| Bug 19 | 70 percent | 0 percent | 0 percent | 0 percent | 0 percent | 0 percent | 0 percent |
| Bug 20 | 0 percent | 0 percent | 20 percent | 0 percent | 80 percent | 0 percent | 0 percent |
Similarly, the team can sort the matrix by rows to see which process changes will be the most likely to detect the bug.
Calculate the Average Effectiveness of Proposed Changes
Now that all the data has been entered in the matrix and reviewed with the team, the modeled effectiveness of each of the proposed process steps can be calculated. The calculation is the average of the individual effectiveness for each of the bugs in the model for a given proposed process change. These averages are listed in the bottom row of Table 1. For example, Proposed Process Change A has a 22 percent probability of catching a bug and Proposed Process Change B only has a 4 percent probability of catching a bug, based on this model. It is important to note that the zero values are part of the average calculation.
Determine a Cumulative Improvement
The final step is to determine the cumulative effectiveness of the entire set of potential process changes in a stepwise fashion. The stepwise cumulative effectiveness is important because it can provide guidance as to which of the potential process changes should be implemented. Also, it can show the point of diminishing returns for the addition of more of the proposed changes.
Steps to determine cumulative effectiveness (Table 3):
- Probability of catching – The first row of the data lists the individual effectiveness of each proposed process change sorted from most to least effective. These are the same numbers as the last row of the completed matrix in Table 1.
- Probability of passing – 100 percent minus the probability of catching.
- Cumulative probability of passing – The cumulative passing rate is calculated starting with the most effective proposed process change, which is located in the left-most column of the table. As proposed process changes are combined, the individual percentages are multiplied. For example, passing rate for change D alone is 65 percent, yet combining changes D and A results in a 50 percent (64 percent x 78 percent) passing rate. Combining changes D, A and H results in a 40 percent (64 percent x 78 percent x 80 percent) passing rate, and so on. There is an underlying assumption that the proposed process improvements are independent.
- Cumulative probability of catching – 100 percent minus the cumulative probability of passing.
| Table 3: Cumulative Improvement Calculations | |||||||
| Proposed Process Changes | |||||||
| Probabilities | D | A | G | C | E | F | B |
| Probability of catching | 36 percent | 22 percent | 20 percent | 18 percent | 15 percent | 7 percent | 5 percent |
| Probability of passing | 64 percent | 78 percent | 80 percent | 82 percent | 85 percent | 93 percent | 95 percent |
| Cumulative probability of passing | 64 percent | 50 percent | 40 percent | 33 percent | 28 percent | 26 percent | 25 percent |
| Cumulative probability of catching | 36 percent | 50 percent | 60 percent | 67 percent | 72 percent | 74 percent | 75 percent |
The cumulative and individual probability of catching bugs also can be shown graphically (Figure 1). Although the first three or four proposed process changes on the left of the graph show significant gains, after that the gains start to plateau. This data, along with other constraints such as difficulty of implementation or resource availability, can guide the decision on what improvements to implement.
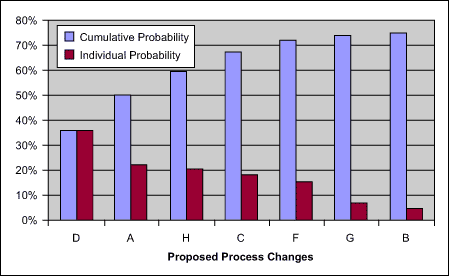
Finding the Value in Modeling
Through this modeling method, practitioners may be able to establish proposed process change effectiveness using historical bug data and the team’s experience. The model result is a bar chart that can be used to guide the decision on what improvements to implement. This technique can be used in situations where running an actual controlled experiment on the process would be difficult.