
As quality professionals, it is easy to become absorbed in day-to-day professional business roles: improving the quality of products or services, increasing productivity, enhancing profits, lowering costs, raising customer satisfaction and so on.
Sometimes, however, it is important to pause and ask ourselves a fundamental question: How are we improving quality in our communities? For quality professionals, this means applying their expertise beyond their paying day jobs to help solve community problems.
Lately, I’ve been volunteering with the Klamath Tribes of Oregon to help in their efforts to restore the Klamath River. I am using my knowledge and skills in statistical process control to help present a more compelling, evidence-based rationale for the removal of four hydroelectric dams along the Klamath River in an effort to help restore the Chinook salmon population. The following case study detailing my work with the tribe serves as an example of how practitioners can use their skills outside the office.
Case Study: Salmon and the Klamath River
The Klamath River runs 250 miles through Oregon and California before empting in the Pacific Ocean. The river was once the third most productive salmon river system in the United States. For more than 300 generations, Indian tribes along the river have fed and sustained themselves on its salmon. In the last 100 years, however, conditions in the Klamath River Basin have changed dramatically. In the early 20th century, four dams were constructed along the river to generate hydroelectric power. Unfortunately, the dams have produced many negative consequences for the salmon: the dams block more than 300 miles of spawning habitat, heat water temperatures to levels lethal to the fish and create reservoirs full of toxic blue-green algae. Consequently, Chinook salmon populations along the Klamath River have been decimated. Today, the Karuk Tribe, for example, harvests only about 400 fish a year.
Enter Statistical Process Control
My volunteer work with the Klamath Tribes involves analyzing salmon population data along the river and interpreting the results. The key tool I utilize is statistical process control – a proven statistical analysis technique used to improve quality and performance.
Two fundamental statistical process control concepts are worth explaining:
1. Variation is the way things normally occur. The amount of variation in a process (i.e., Chinook fall salmon migration) tells what that process is actually capable of achieving. There are two types of variation:
- Random – Variation that occurs naturally is always present to some degree in a process. For example, in any given year the timing and population of fall spawning salmon migration might vary due to weather conditions, ocean temperatures or currents, available food supply, or natural salmon predators. In Six Sigma, this type of variation is called common cause.
- Non-Random – Variation caused by a non-random event, an action, or a series of events or actions. For example, the construction of the hydroelectric dams on the Klamath River in the early 20th century. In Six Sigma, this is special cause variation.
Table 1 summarizes the two forms of variation and the strategies for managing both.
| Table 1: Characteristics of Variation and Strategies for Management | ||
| Variation | Characteristics | Strategy to Manage |
| Random | • Inherent in a process • Expected over the long-term |
Continually and gradually improve the stable process |
| Non-random | • Specific to an event or crisis • Driven by something outside of the normal process • Not predictable |
• Respond to the crisis • Take immediate action to respond to the correct issue • Identify and remove the causes |
2. Control Charts plot observations over time. These charts are used to monitor, control and improve process performance by studying variation and its source. A control chart consists of a centerline (i.e., mean) and upper and lower control limits that are set by the process itself.
Control charts can be used to determine whether common or special causes are present in the Klamath River. The general rules for interpreting control charts are:
- If all the data points are located inside the control limits fairly close to the centerline, common causes are present. Hence, practitioners can conclude the process is statistically “in control” (i.e., within three standard deviations of the mean). An in control process is stable and predictable. Accordingly, the strategy to manage such a process is to continually and gradually improve the stable process.
- Any point lying on or outside of either control limit indicates the presence of special causes. Hence, the process is not statistically in control and cannot be considered stable or predictable, and assessments of the capability or future performance of the process cannot be made. Accordingly, the strategy to manage such a process is to immediately identify the special causes and remove them.
Table 2 shows 30 years of data for the adult Chinook salmon population entering the Klamath River (source: 2007 Review of Ocean Salmon Fisheries study, February 2008).
| Table 2: Chinook Salmon Population By Year | |||
| Year | Population | Year | Population |
| 1978 | 92,983 | 1993 | 57,212 |
| 1979 | 51,295 | 1994 | 63,983 |
| 1980 | 45,640 | 1995 | 222,768 |
| 1981 | 80,292 | 1996 | 175,773 |
| 1982 | 66,612 | 1997 | 83,736 |
| 1983 | 57,546 | 1998 | 90,647 |
| 1984 | 47,261 | 1999 | 51,048 |
| 1985 | 64,438 | 2000 | 218,077 |
| 1986 | 195,019 | 2001 | 187,333 |
| 1987 | 209,134 | 2002 | 160,788 |
| 1988 | 191,642 | 2003 | 191,948 |
| 1989 | 124,340 | 2004 | 79,191 |
| 1990 | 35,882 | 2005 | 65,227 |
| 1991 | 32,670 | 2006 | 61,374 |
| 1992 | 26,698 | 2007 | 130,506 |
I developed an individuals control chart (see figure below) based on the data in Table 2. To achieve normality, the data was transformed using the natural log (lambda = 0).
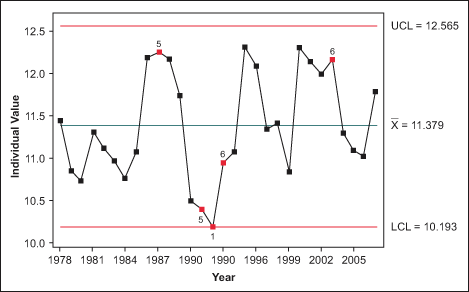
Notice the extreme variation around the centerline (mean). Several points are located near or on the control limits (red points). This indicates the presence of special causes. The specific tests for special causes are:
- One point is more than 3.00 standard deviations from center line. Test failed at point: 15
- Two out of three points are more than two standard deviations from center line (on one side of center line). Test failed at points: 10, 14, 15
- Four out of five points are more than one standard deviation from center line (on one side of center line). Test failed at points: 16, 26
Based on these test failure points, the Chinook salmon population in the Klamath River is not stable or predictable. In response, the special causes must be immediately identified and removed. This would entail removing the four hydroelectric dams and restoring the river to its pre-dam condition.
Putting Talent to Use
Quality professionals are blessed with unique skill sets and knowledge in disciplines such as statistical quality control, Six Sigma, Lean and industrial engineering. We have an opportunity and social responsibility to leverage those talents to make a difference in our communities.