
Newspapers face pressure from their external customers to minimize the cycle time of their production process at both ends of the supply chain. At the start of the chain, readers want the freshest news, while advertisers want the latest possible closing time for booking ads. At the end of the chain, even a few minutes of delayed delivery can result in unsold market returns.
Editor’s note:
This article is Part 3 of a series on a TQM deployment at a mid-sized Indian newspaper company.
Part 1 covers improvements made to product quality. Part 2 describes changes made to customer service.
Often, purchase decisions are made in short, fixed windows of time or on the spur of the moment – while waiting for the morning bus or train, during the short walk to the office, or when a vendor taps on the car window at a red light. In short, newspaper delivery must be neither late nor early, and it must be completed in a minimum amount of time.
This last article in a three-part series illustrates how TQM was used to make cycle time improvements throughout the newspaper’s supply chain in order to ensure efficient and on-time delivery.
Defining the Problem
At this particular company, newspapers were not always delivered to sales stalls on time, which was resulting in lost circulation and waste due to market returns. In TQM, the equation to define a problem is:
Problem = Desire – Actual status
In this case, the desire was for the newspapers to arrive at all depots at or before each depot’s fixed target time every day. At the start of the project, the company had no measured actual status. To gain this data, the team measured truck arrival times at each depot for one week, and calculated the deviation from targets. Negative deviation denoted early arrivals and positive numbers represented late arrivals.
The team determined the following from their analysis:
- Deviation from target time for individual depots = d = 11 min.
- Average of deviations for all d’s for one day = a
- Average of a over several days = D = 11 min.
- Standard deviation, or sigma, of d = s = 33 min.
- Sigma of D = S = 17 min.
- Delivery delay within three standard deviations for individual arrivals = d + 3s = 110 min.
- Daily average delivery delay within three standard deviations = D + 3S = 62 min.
For the daily average to achieve a 3 sigma standard (99.7 percent on-time delivery), the 62 minutes had to be reduced to zero. For individual arrivals to be consistent, 110 minutes also had to be reduced to zero. The team decided to attempt the improvement in two phases: improve by 50 percent in the first phase, and then improve to zero in the second.
Analyzing the Process
The team analyzed the causes of delayed delivery at the end of a supply chain using process mapping. This involved:
- Identifying the start and end points of the process, the latest cut-off start time and the expected delivery time.
- Mapping all value-added and non-value-added activities.
- Determining the standard cycle time and cut-off delivery time of each stage.
- Timing the actual flow of activities through the process.
- Identifying the stages where delays occur and the causes.
The newspaper production cycle has two basic work streams: building pages that contain only ads and building pages that contain both ads and editorial material (Figure 1). In the figure below, the cycle for ad pages is shown in green. The cycle for pages that require simultaneous processing of ads and editorial material are shown in the blue and orange boxes. The final activity is shooting the pages to the press for printing, with a deadline time set for each page.
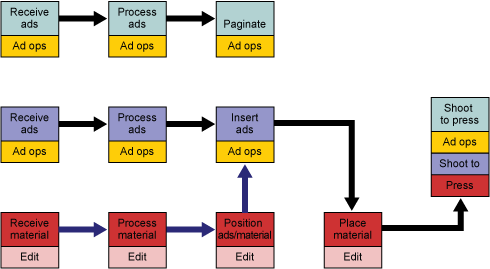
Once the pages are sent to the press, the newspapers are printed and copies are sent to the depots (Figure 2).

The newspaper chain is geared for designing, producing, delivering and selling a product within hours. This fast pace made improvement seem a daunting task. The team decided to use a segmented approach: Pick the weakest link and strengthen it, then pick the next weakest and so on until the objective is achieved.
Finding the Weakest Link
The team timed the longest chain of printing and dispatching at key points and compared them against targets (Table 1).
| Table 1: Printing Process Time Over Six Days | ||||||
| Day 1 | Day 2 | Day 3 | Day 4 | Day 5 | Day 6 | |
| Line 1 – time of start of printing vs. schedule | 10 minutes ahead | 10 minutes ahead | 16 minutes ahead | 3 minutes ahead | 5 minutes behind | 5 minutes ahead |
| Line 2 – time start of printing vs. shedule | 1 minute ahead | 9 minutes ahead | 4 minutes ahead | 15 minutes behind | 22 minutes ahead | 27 minutes ahead |
| Time printing finished vs. schedule | 15 minutes ahead | 36 minutes ahead | 24 minutes ahead | 11 minutes ahead | 30 minutes ahead | 44 minutes ahead |
Manufacturing processes often are blamed for delays. Here, however, despite occasional upstream delays, printing finished each day with a few minutes to spare. Therefore, the team looked elsewhere to find the weakest link.
The next area they investigated was delivery to the depots. For all deliveries to take place on time, 14 trucks needed to reach between 70 and 100 delivery points punctually. This was not the case; delivery times are shown in Table 2.
| Table 2: Delivery Time Delays | ||
| Truck Departure (D) Time vs. Schedule | Truck Arrival (A) Time vs. Schedule | |
| Average | 2 minutes behind | 5 minutes behind |
| Standard deviation (sigma) | 21 minutes | 23 minutes |
| Average + 3 sigma | 66 minutes behind | 64 minutes behind |
These numbers indicated that the hold-up was due in part to delayed truck departure, despite on-time printing. After observing 84 deliveries, the team noticed that, 90 percent of the time, the first five trucks left late, while only 6 percent of the last five dispatches left late each day (Table 3).
| Table 3: Delivery Time Sample Divided by Truck Group | ||||
| Total | Trucks 1-5 | Trucks 6-9 | Trucks 10-14 | |
| On time | 39 | 3 | 8 | 28 |
| Delayed | 45 | 27 | 16 | 2 |
| Total | 84 | 30 | 24 | 30 |
| Percent on time | 46 | 10 | 33 | 94 |
To determine why this was happening, the team examined the process of bundling the two sections of the paper. Section A was pre-printed and kept in machine-counted bundles of 50. Section B also was coming off the line in machine-counted bundles of 50. The paper needed to have Section A inserted in Section B. Each truck had two kinds of bundles:
- Count 50: Machine-counted bundles of A and B were strapped and sent separately to be merged at the delivery point.
- Odd count (less than 50): Machine-counted stacks were broken, counted, merged and strapped for loading on to the trucks.
The bundling was being done in batch mode:
- For the first 20 to 30 minutes after a print run started, workers stacked bundles of 50 for use in creating the odd-count bundles.
- After 30 minutes, workers loaded standard bundles of 50 into each truck as per order.
- Each truck waited until it had the correct mix of bundles loaded.
The loss of 20 minutes in the beginning meant delays for the earlier trucks until the manual process caught up.
Generating Countermeasures
The printing machine output was a continuous flow. All operations up to trucking were re-designed as a flow as follows:
- Bundles built per minute: 6
- Fraction of bundles that were non-standard: 0.3
- Non-standard bundles built per minute: 1.8
The team identified trucks that had a higher ratio of non-standard bundles, so a second group of workers was brought in for these trucks to ensure flow. The sequence of trucks was adjusted to suit the timing of the trucks at their first drop points.
The organization conducted two weeks of trials for this new process (Table 4).
| Table 4: Delays Before and After Flow System Implementation | ||||
| D Before | A Before | D After | A After | |
| Average | 2 minutes behind | 5 minutes behind | 20 minutes ahead | 15 minutes ahead |
| Standard deviation | 21 minutes | 23 minutes | 5 minutes | 4 minutes |
| Average + 3 sigma | 66 minutes behind | 64 minutes behind | 5 minutes ahead | 3 minutes ahead |
To standardize the process, the team prepared standard operating procedure documents and trained process owners to run the line in flow, measure and review the average + 3 sigma numbers each week, and kill any new problems that might occur.